
|

|
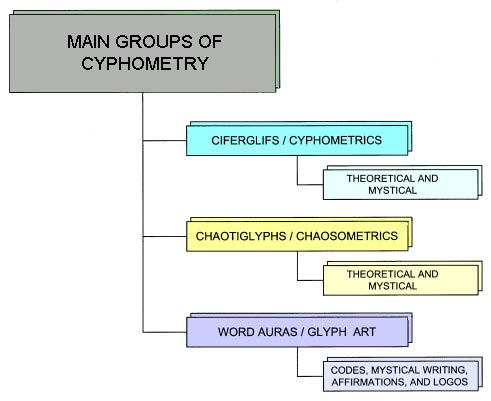
The present invention relates generally to cryptographic codes and puzzles and, more specifically, to cyphometry consisting of ciferglifs, chaotiglyphs and word auras. Cyphometry is an esoteric mathematical system that is the direct result of a comparative study of the complex geometric patterns that are formed through specific adding formulas within its fixed number scales between the digits zero (0) and nine (9), hereinafter referred to as the cyphometric number scale. Ciferglifs are created by using a fixed number scale (cyphometric number scale), All ciferglifs are made up of smaller geometric structures, primarily offset tetrahedrons and triangles. All ciferglifs fit together like a puzzle in form or fashion. Ciferglifs in this way illustrate geometrically the concept of connectivity much like letters within the English alphabet. Example: the letters "L" and "F" can be found within the letter "E". The present invention, word auras are an abstract esoteric art form that utilize the three basic forms of written communication, numbers, letters and symbols. Any word in any written language can be given a numerical value and that number value can be translated into a geometric design or symbol. Taking a word and translating it into a number then transforming that number into a symbol. It is a kind of systematic fusion between mysticism and science, the impractical with the practical. Also word auras are a code system that can mutate like a virus, without changing its structure.
As attorney for the inventor of Cyphometry Consisting of Ciferglifs Chaotiglyphs & Word Auras we are currently seeking investors and manufacturing companies to license, purchase patent rights or enter into a royalty agreement for this timely invention. Interested parties can reach the attorney at the contact numbers listed at the bottom of this page. |
|
The following pictures are meant to display possible physical characteristics of the present invention and are not to be taken in a limiting sense. It is understood that other embodiments may be utilized and that structural changes may be made without departing from the scope of the invention.
More Of Cyphometrics

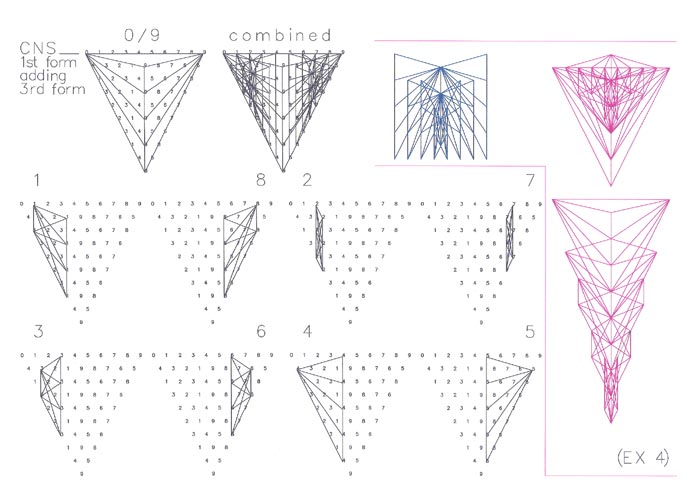
Patent Drawings
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
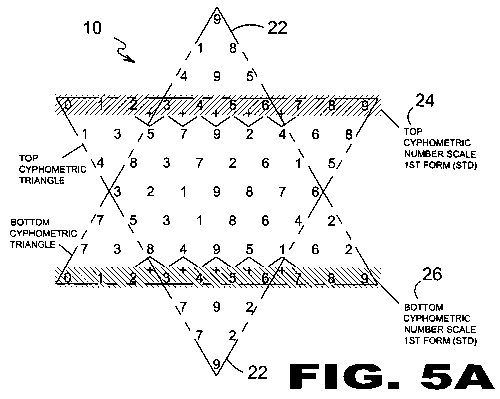 |
| FIGURE 5A Figure 5A is an illustrative view of space adding resulting in a Cyphometric Triangle (22). Illustrated is a pair of Cyphometric Triangles (22) that can pass through one another and maintain their individual forms starting at the top Cyphometric Number Scale (24). The top Cyphometric Triangle (22) utilizes the 1st (standard) form for adding, and the bottom Cyphometric Triangle (22) utilizes the 5th (adverse-reactive) form for adding. This illustration depicts an abstract numeric reasoning as to how two dimensions can be within or side by side one another at different vibratory frequencies. |
|
 |
|
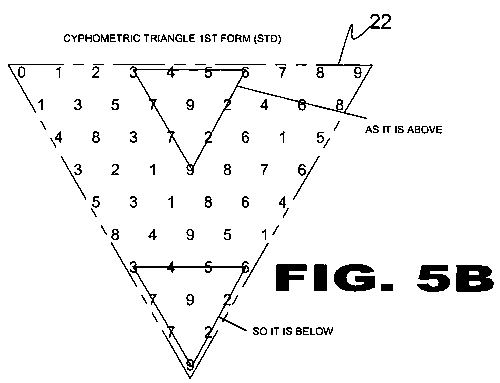
| FIGURE 5B Figure 5B is an illustrative view of an abstract numeric reasoning of a Cyphometric Triangle (22). Illustrated above is a depiction of an abstract numeric reasoning for the ancient mystic concept that states "as it is above, so it is below". |
|
 |
|
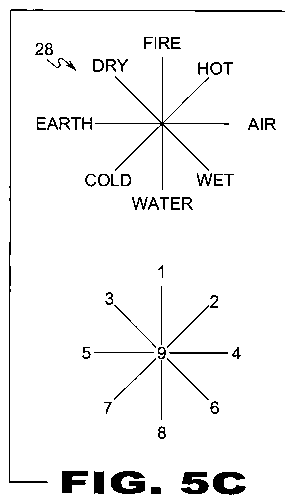
| FIGURE 5C Figure 5C is an illustrative view of the concept of duality according to cyphometric opposites. The illustration above expresses a basic compact concept of duality in relation to the world in which we live in accordance to Cyphometric Opposite Numbers (28). |
|
 |
|
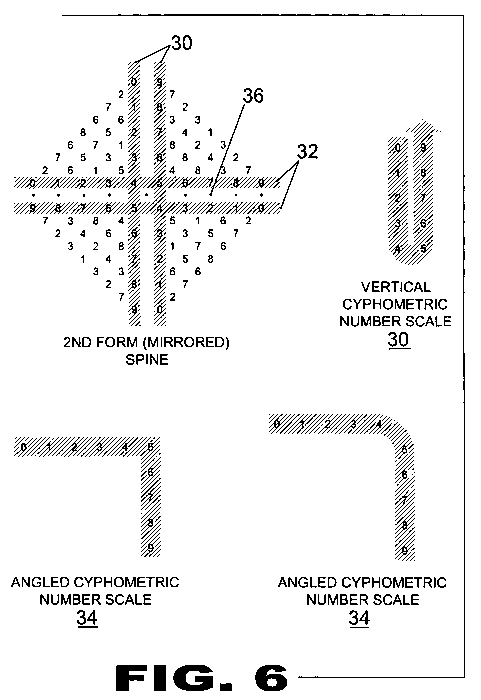
| FIGURE 6 Figure 6 is an illustrative view of various forms of Cyphometric Number Scale (20). Shown are various forms of the Cyphometric Number Scale (20). The Cyphometric Number Scale (20) may be oriented in many ways as long as the scale begins with (0/9) and ends in (9/0). Also shown are points or "Disks (36)". Disks (36) can be shared by any number and its opposite within the Spine (74). |
|
 |
|
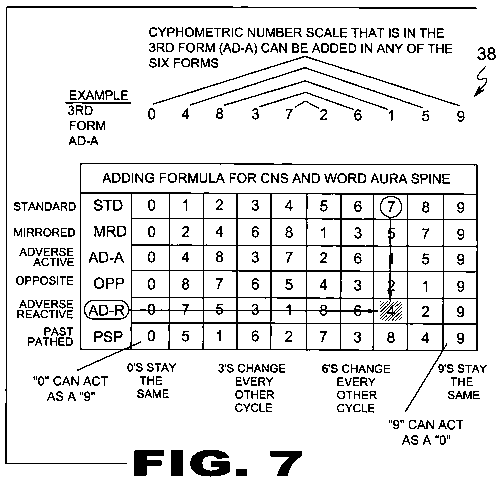
| FIGURE 7 Figure 7 is a chart for the adding formula for the Cyphometric Number Scale (38) and word aura Spine (74). Shown is the adding formula for CNS and word aura Spine (74). When working with either, the math is the same, any two numbers that are added together are, if necessary, reduced to a single digit. That sum is described in standard 1st form which is also the Cyphometric Number Scale (20) (0 thru 9). To identify the value of a number in another form, the intersection of the column and row is used. Example: 4+3 = 7. To find the adverse-reactive equivalent to 4+3, go to the column of the 1st form sum (7), move down the column until the adverse-reactive (5th form) row is reached at the left. The resulting adverse-reactive value of 4+3 is equal to 4. Furthermore, each code form row is a Cyphometric Number Scale (20) because they begin with 0/9 and end with 0/9, and the numbers in between are opposites of each other at any given point within the scale. However, 0 and 9 are not always used. |
|
 |
|
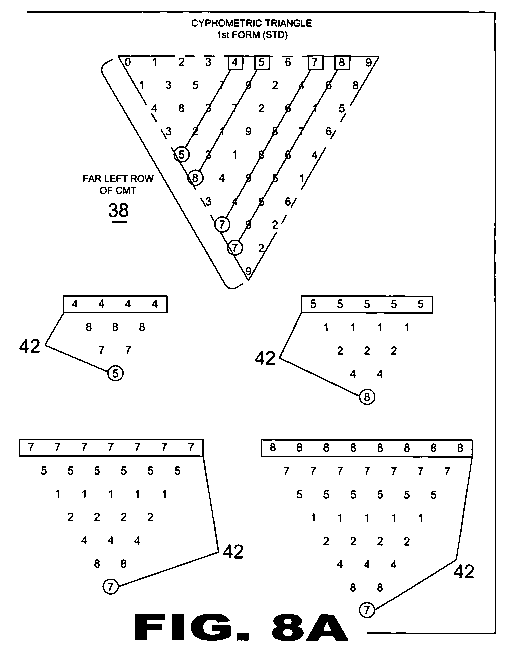
| FIGURE 8A Figure 8A is an illustrative view describing the derived code forms relationship (42) between the Cyphometric Number Scale (20) and the far left row of the cmt. The above examples depict that any number within the Cyphometric Number Scale (20) that has its quantitative value of itself spaced added will result in the last number of the far left row of the cm triangle. |
|
 |
|
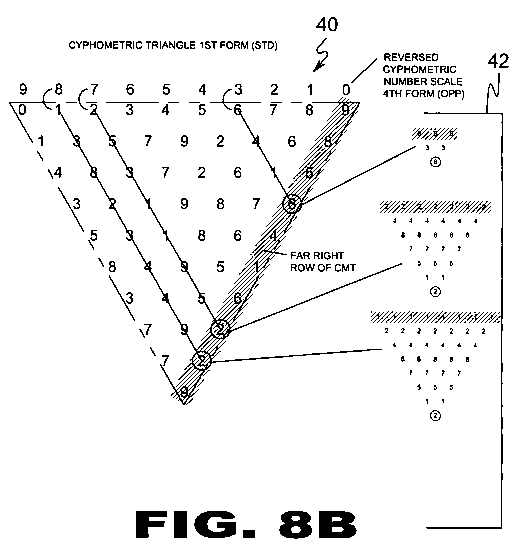
| FIGURE 8B Figure 8B is an illustrative view describing the derived code forms relationship (42) between the reversed Cyphometric Number Scale (20) and the far right row of the cmt. The above examples depict that by adding the reversed Cyphometric Number Scale (20) (4th form opposite) above the Cyphometric Number Scale (20) in the first form (std) and has its quantitative value of itself space added will result in the last number of the far right row of the Cyphometric Triangle (22). Three sixes, seven twos, and eight ones. |
|
 |
|
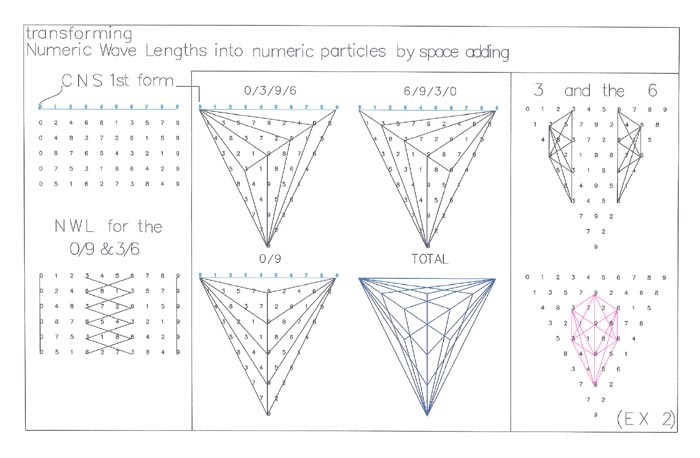
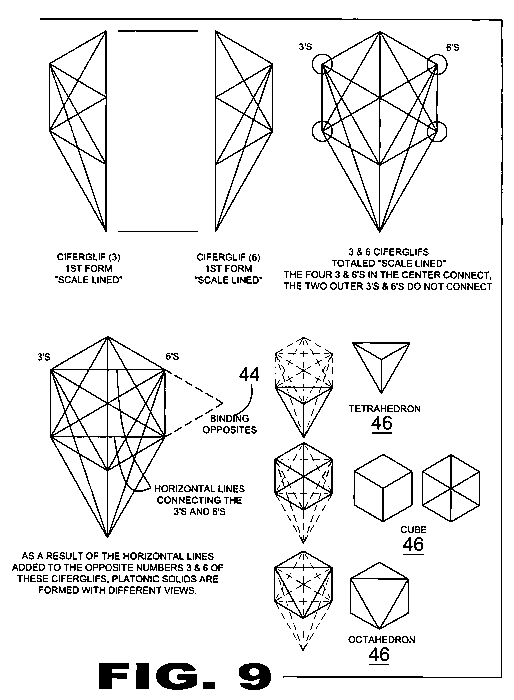
| FIGURE 9 Figure 9 is an illustrative view of the 3 and 6 Ciferglifs (12) in the 1st form depicting Binding Opposites (44) to create Platonic Solids (46). All Ciferglifs (12) can connect to each other in some fashion and lines can be added to the numbers that are not connected as long as they are opposites (1 & 8) (2 & 7) (3 & 6) or (4 & 5). This connection is called binding. |
|
 |
|
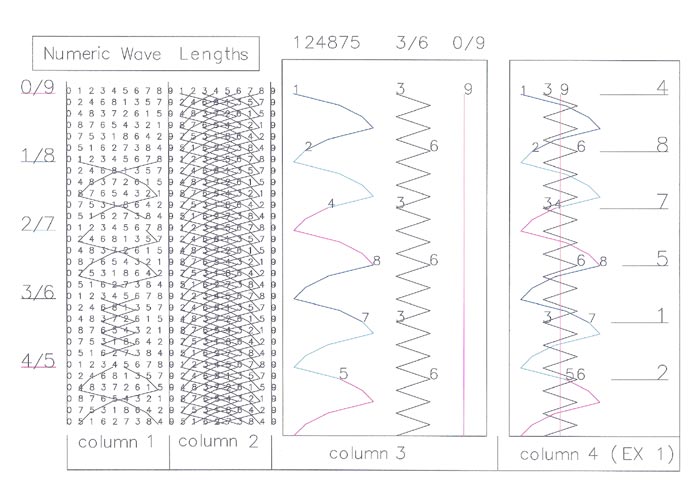
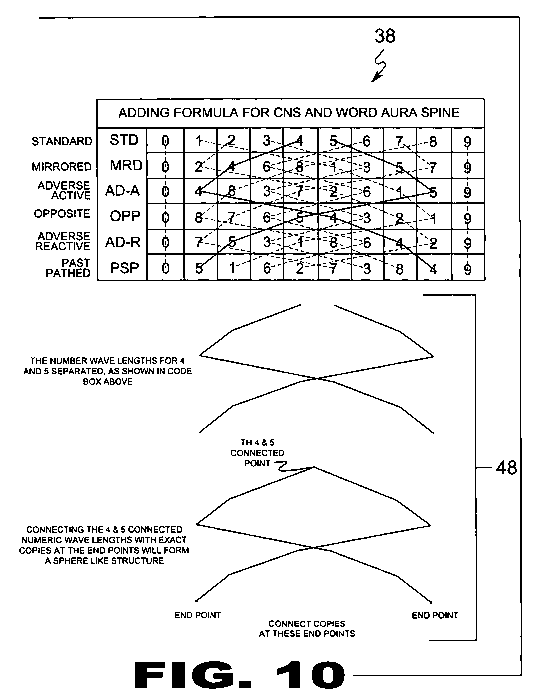
| FIGURE 10 Figure 10 is an illustration depicting a chart for the adding formula used to create Numeric Wave Lengths (48). Ciferglifs (12) depict solids, using the different code forms, however, you can create a sphere like structure by changing the code into what are called Numeric Wave Lengths (48). Numeric Wave Lengths (48) are created by connecting like numbers. Like Ciferglifs (12), the formed Numeric Wave Lengths (48) are opposites. Depicted above shows a #4 wave length and #5, its opposite. |
|
|
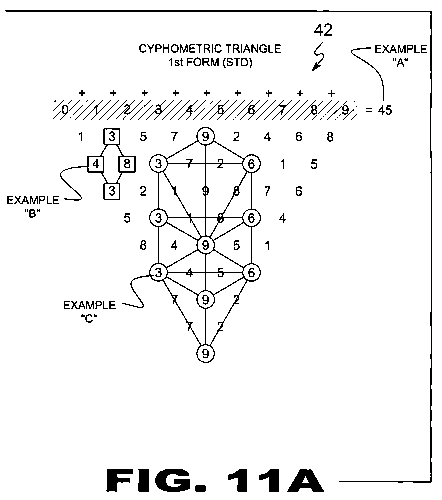 |
| FIGURE 11A Figure 11A is an illustrative view describing the derived code forms relationship (42) within the Cyphometric Number Scale (20) and the Cyphometric Triangle (22). Example "A" denotes all cn scales add to a total of 45. Additionally there is six of each numeral in the Cyphometric Triangle (22), of which when added, the sum is always equal to 270 (270 / 6 = 45). Example "B" denotes a repetitive sum of 9. Whether vertical, horizontal or diagonal, when any four numbers are added together forming a diamond shape, the sum will always be 9 when broken down to a single digit. Example "C" denotes "the tree of life", ancient mystic Jewish symbol of the structure of god / creation. The symbol is made from the numbers 3, 6, and 9. Individual Ciferglifs (12) can make this structure with a multidimensional view. |
|
 |
|
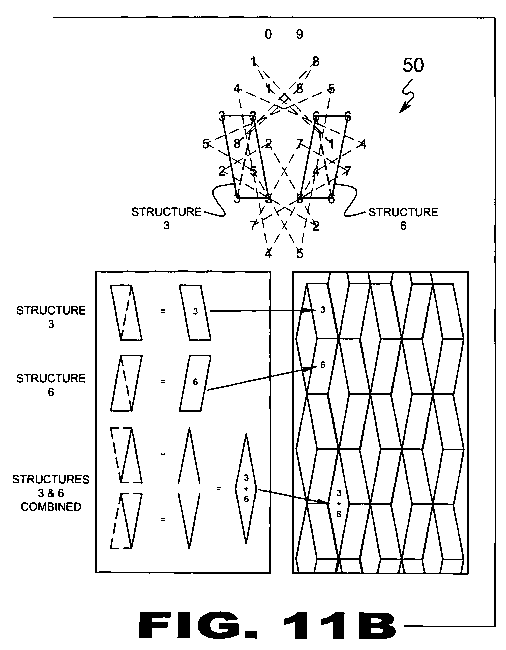
| FIGURE 11B Figure 11B is an illustrative view describing a common form of Periodic Tiling (50). Cyphometry (10) is a non-conventional geometry, however, one can create many practical applications such as tiling in an abstract way. The upper illustration depicts a Cyphometric Number Scale (20) ordered in the same fashion as with cell numbers (76) in Word Auras (18). Using 1/4 of the full structure and select lining. (note: by using only the structures made by 3 and 6, one can create a simple form of Periodic Tiling (50). Periodic Tiling (50) is depicted in the lower illustration. |
|
 |
|
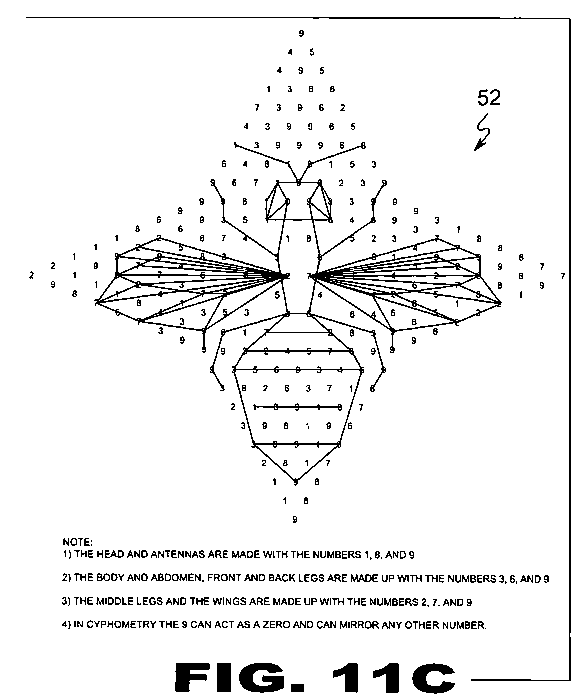
| FIGURE 11C Figure 11C is an illustrative view of an insect composed of lined opposite numbers with straight lines. The figure is formed by using the same structure from figure 11b which is a vertical Cyphometric Number Scale (30) added on both sides in the 1st form (std), spaced added, and again spaced added on the four sides to form a square and yet spaced added once more on the flat sides of the square to form a four pointed star. The end result in lining opposite numbers in this instance, becomes an insect. |
|
 |
|
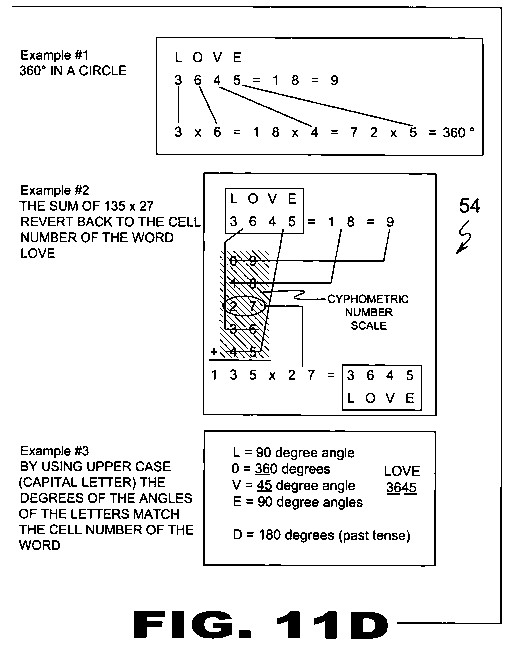
| FIGURE 11D Figure 11D is an illustrative view describing cyphometry (10) as a mathematical system that expresses a Numeric Theology (54). Cyphometry (10) as a mathematical system that expresses a Numeric Theology (54) by using an abstract methodology to the 3 basic forms of written / oral communication; numbers, letters, and symbols. It has been said that "love is what makes the world go round". As depicted in the illustrations above, by using basic cyphometry (10), one can find a numeric reasoning for this thought. |
|
 |
|
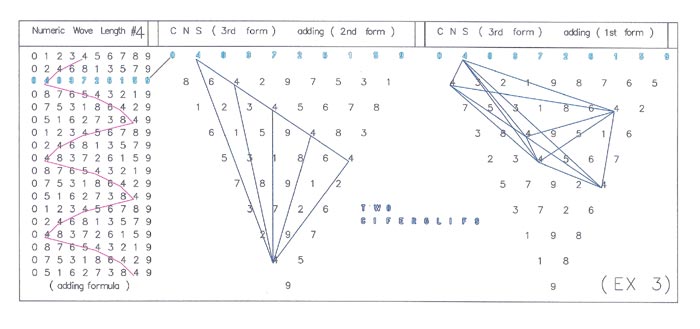
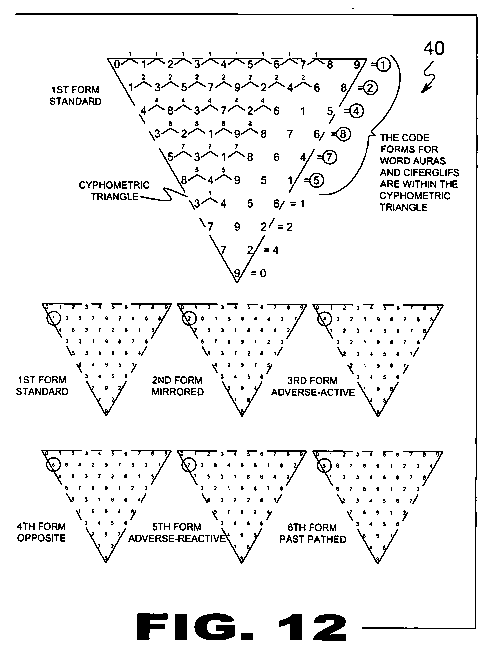
| FIGURE 12 Figure 12 is an illustrative view describing the derived code forms. Depicted are the Code Forms (40) for Word Auras (18) and Ciferglifs (12). The Code Forms (40) are derived from the Cyphometric Triangle (22) in the 1st standard form. By spaced adding the numbers of each row in the same single digit format, each of the first six rows depict a single repetitive digit that is in turn used to identify the code form. Note: the repeat digit is represented in each of the Code Forms (40) in the same position within the Cyphometric Triangle (22). Note: all six adding formulas shown above are depicted with the Cyphometric Number Scale (20) being in the 1st form (std). The other forms can be used as well. |
|
 |
|
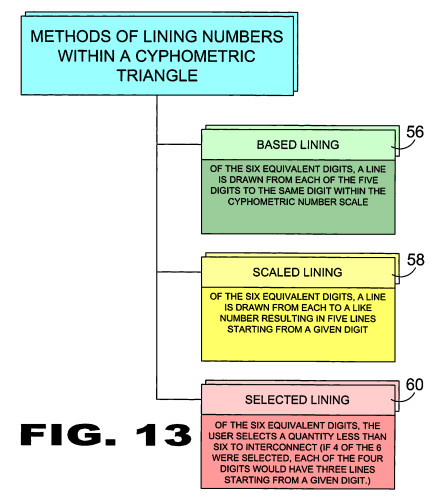
| FIGURE 13 Figure 13 is a block diagram of the basic methods of lining within a Cyphometric Triangle (22). The basic methods of lining within a Cyphometric Triangle (22) are Based Lining (56), Scaled Lining (58), and Selected Lining (60). Selected Lining (60) is particularly useful in developing Platonic Solids (46) from Ciferglifs (12). |
|
 |
|
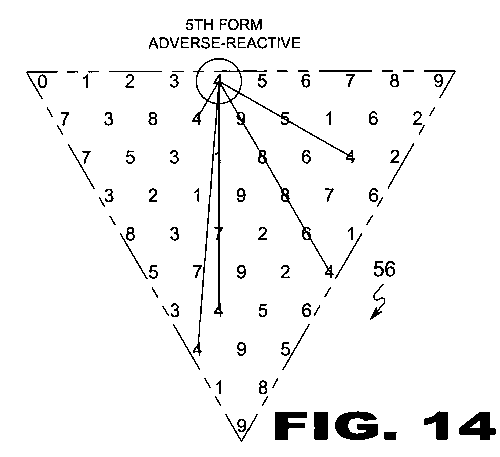
| FIGURE 14 Figure 14 is an illustrative view of the method of Based Lining (56) within a Cyphometric Triangle (22). There are six of each digit within a Cyphometric Triangle (22). Each digit has its own unique pattern in each of the six code forms. In the method of Based Lining (56), a line is drawn from each of the five digits to the same digit within the Cyphometric Number Scale (20). Illustrated is the number 4 based lined in the 5th form. |
|
 |
|
| FIGURE 15 Figure 15 is an illustrative view of the method of Scaled Lining (58) within a Cyphometric Triangle (22). There are six of each digit within a Cyphometric Triangle (22). Each digit has its own unique pattern in each of the six code forms. In the method of Scaled Lining (58), a line is drawn from each to a like number resulting in five lines starting from a given digit. Depicted above is the number 4 scaled lined in the 5th form. |
|
 |
|
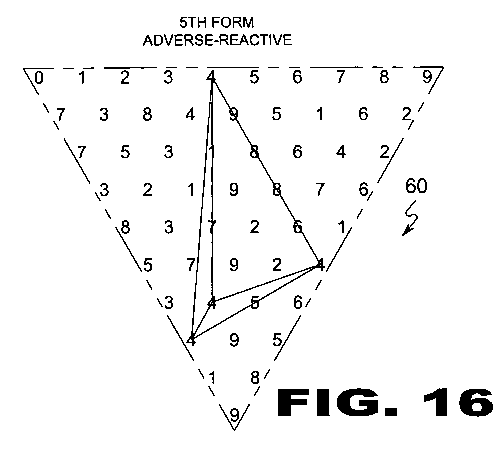
| FIGURE 16 Figure 16 is an illustrative view of the method of Selected Lining (60) within a Cyphometric Triangle (22). There are six of each digit within a Cyphometric Triangle (22). Each digit has its own unique pattern in each of the six code forms. In the method of Selected Lining (60), the user selects a quantity less than six to interconnect. Depicted is a quantity of 4 of the number 4 selected lined in the 5th form. Selected Lining (60) is particularly useful in developing Platonic Solids (46) from Ciferglifs (12). |
|
 |
|
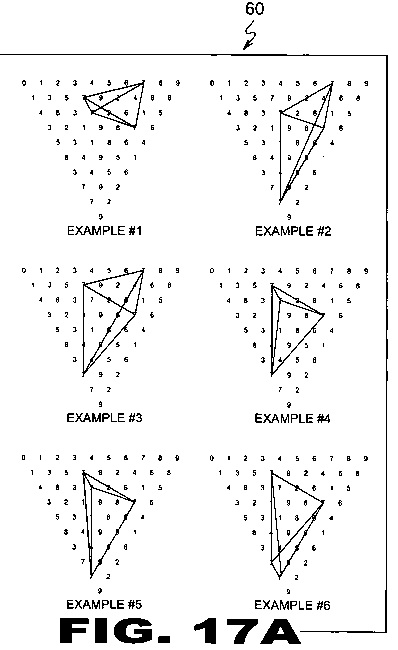
| FIGURE 17A Figure 17A is an illustrative view of the method of Selected Lining (60) within a Cyphometric Triangle (22). All Ciferglifs (12) as well as Chaotiglyphs (16) are made up of smaller geometric structures, primarily offset tetrahedrons and triangles. Each Cyphometric Triangle (22) and chaosometric triangles (64) will vary depending on the adding formula it's in. Illustrated are Cyphometric Triangle (22)s in the 1st adding form (standard) and using the ciferglif for the number 7 select lined. |
|
 |
|
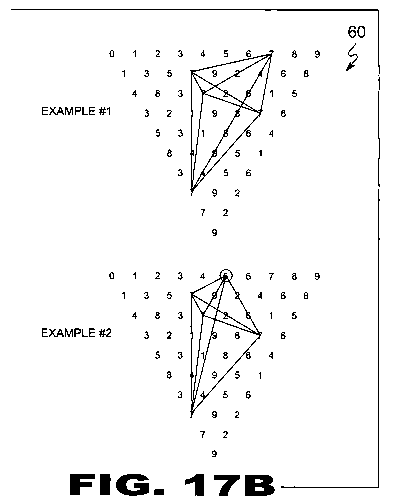
| FIGURE 17B Figure 17B is an illustrative view of the method of Selected Lining (60) within a Cyphometric Triangle (22) to form "alternate Ciferglifs (12)". We have established lining "like" numbers within the Cyphometric Triangle (22) (7's with 7's, 8's with 8's) as shown in sample 1. However, one can line numbers in correlation to the adding formulas themselves, to create what is called "alternate Ciferglifs (12)". Using the number 5 within the (CNS) in example 2, the past pathed or 6th form of that number is 7. Simply, lines are drawn from the 5 to the 7's in a select manner for this illustration. |
|
 |
|
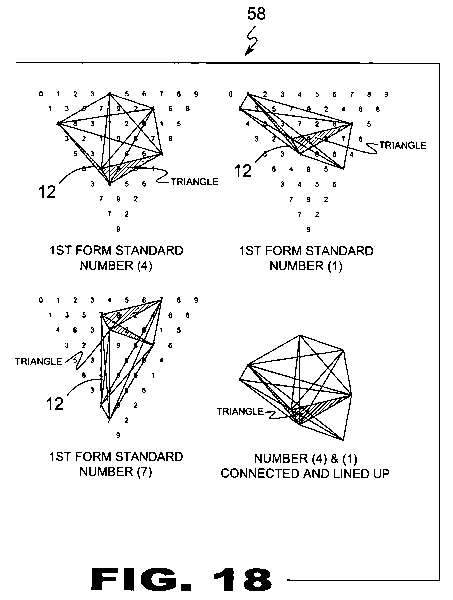
| FIGURE 18 Figure 18 are illustrative view of the method of scale lining within a Cyphometric Triangle (22). Depicted is a Ciferglifs (12) in the 1st form standard with scale lining for the numbers, 4, 1, and 7. The numbers 5, 8, and 2 are identical but mirror image because they are opposites. Shaded are triangle forms that repeat. The image at the bottom right shows these triangles from number 1 and 4 lined up. Note, even the symbols for these numbers are opposites. The 4, 1 and 7 are made up of only straight lines. Their opposites, 5, 8 and 2 have curves. |
|
 |
|
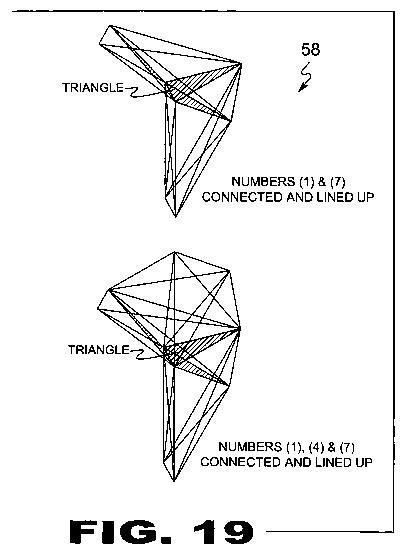
| FIGURE 19 Figure 19 is an illustrative view of the method of scale lining within a Cyphometric Triangle (22). Depicted are Ciferglifs (12) in the 1st form standard with scale lining for the numbers, 4, 1, and 7. All Ciferglifs (12) fit together like a puzzle in form or fashion. Ciferglifs (12) in this way illustrate geometrically the concept of connectivity much like the letters within the English alphabet. Example: the letters "L" and "F" can be found within the letter "E". |
|
 |
|
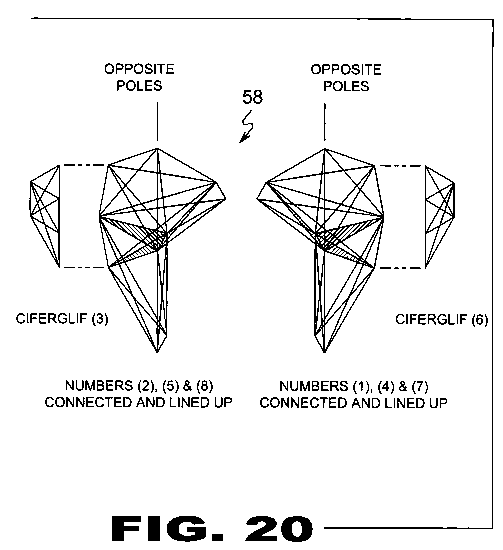
| FIGURE 20 Figure 20 are illustrative view of the method of scale lining within a Cyphometric Triangle (22). Depicted is a Ciferglifs (12) in the 1st form standard with scale lining for the numbers 4, 1, and 7. The numbers 5, 8, and 2 are identical but a mirror image because they are opposites. Shaded are triangle forms that repeat. Also shown are Ciferglifs (12) for 3 and 6 which also mirror each other. |
|
 |
|
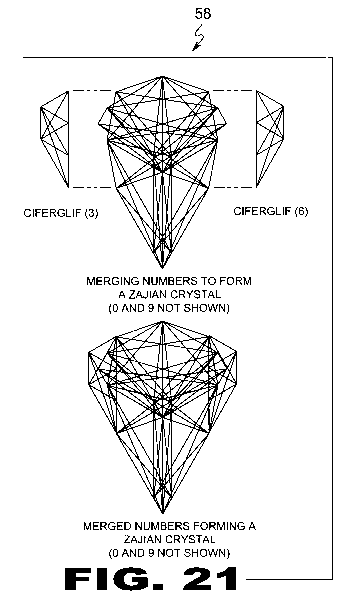
| FIGURE 21 Figure 21 is an illustrative view of the method of scale lining within a Cyphometric Triangle (22). Depicted are Ciferglifs (12) in the 1st form standard with scale lining for the numbers 3, 4, 1, and 7. The numbers 6, 5, 8, and 2 are identical but a mirror image because they are opposites. When connected at common poles, a Zajian crystal is formed. |
|
 |
|
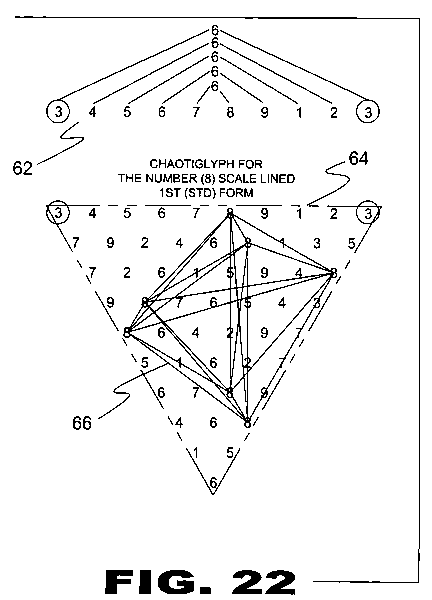
| FIGURE 22 Figure 22 is an illustrative view of the method of creating a Chaotiglyph (66). We have established that Ciferglifs (12) are created by using a fixed number scale (Cyphometric Number Scale (20)), Chaotiglyphs (16) on the other hand, utilize a Chaosometric Number Scale (62). A Chaosometric Number Scale (62) does not utilize the number (0) and must end with the number it began the sequence with. The same side adding principals apply in creating the Chaosometric triangle (64). Depicted is the Chaosometric Number Scale (62) that begins and ends with the number (3) and a scale lined Chaotiglyph (66) for the number (8) is created. Note: in the case of this Chaosometric Number Scale (62) that begins with 3 and ends with 3, the total being 6, the numbers in between at both ends of the scale also add to 6. |
|
 |
|
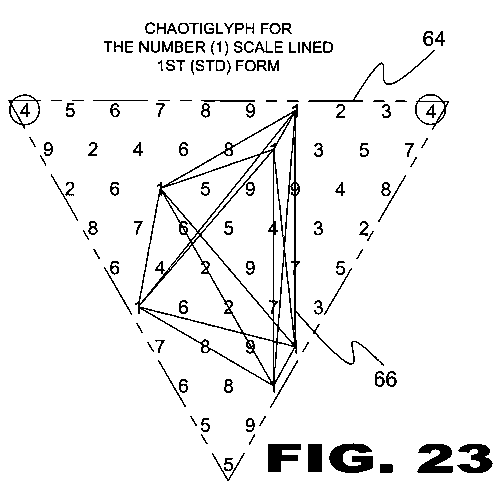
| FIGURE 23 Figure 23 is an illustrative view of the method of creating a Chaotiglyph (66). Depending on the form of a Chaosometric triangle (64) is in, they can create Ciferglifs (12) by using different numbers and are generally angled and can even be upside down. This is depicted in the above Chaosometric triangle (64) with number 4 to 4. The structure is a ciferglif that is created when the Cyphometric Number Scale (20) is added in the 5th form (ad-r) using the number 4. But with the Chaosometric triangle (64), the Chaotiglyph (66) made with the number 1 is upside down and to the left. The number 1 is the (ad-r) using the number 4. Its counterpart is referenced in figure 15. |
|
 |
|
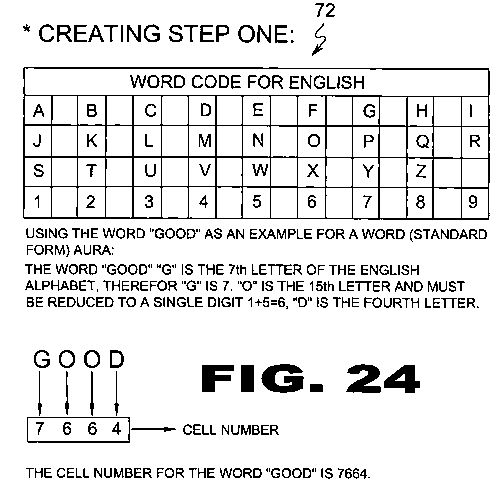
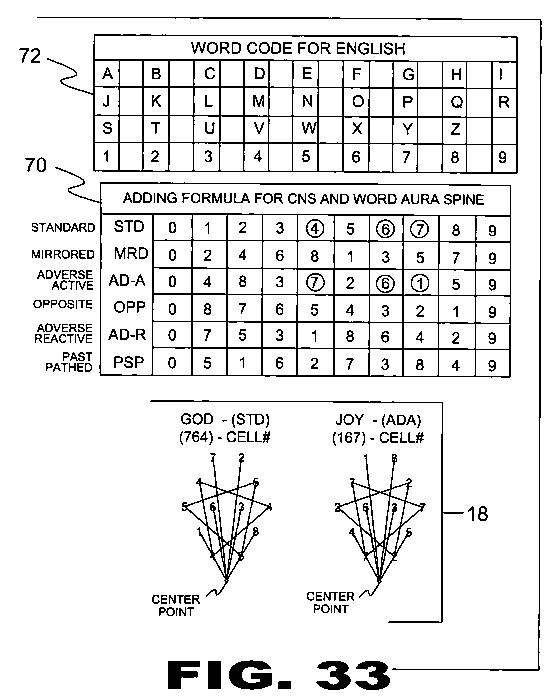
| FIGURE 24 Figure 24 is step one of the present invention. Word Auras (18): are the only esoteric art in the world that combines the three basic forms of written communication, numbers, letters and symbols to form complex geometric designs derived from the numerical values given to the letters of words. The Word Code (72) depicted above is the preferred arrangement of letters of the alphabet, other arrangements may be defined to create different codes and would result in different shaped Word Auras (18). |
|
 |
|
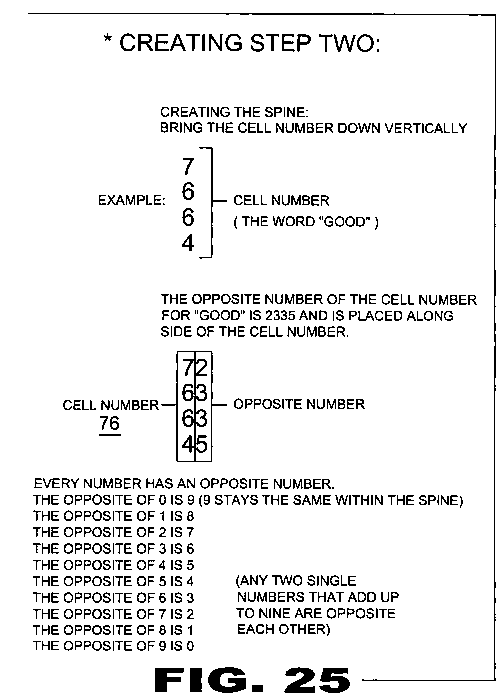
| FIGURE 25 Figure 25 is step two of the present invention. |
|
 |
|
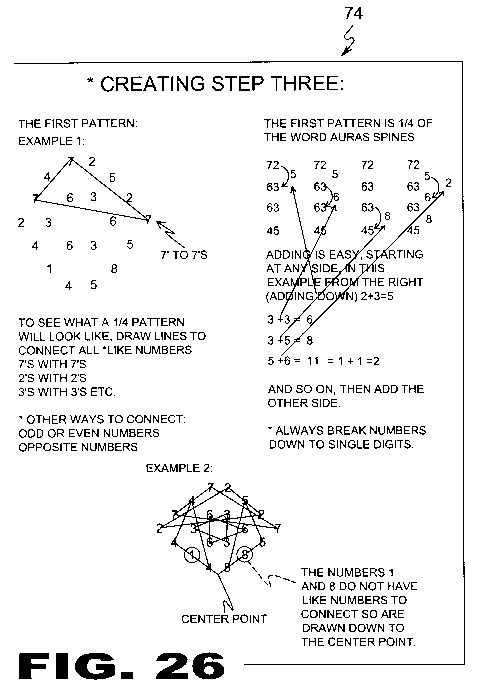
| FIGURE 26 Figure 26 is step three of the present invention. |
|
 |
|
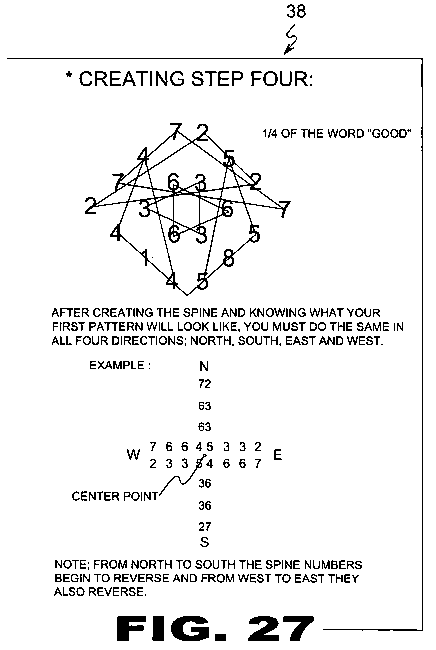
| FIGURE 27 Figure 27 is step four of the present invention. |
|
 |
|
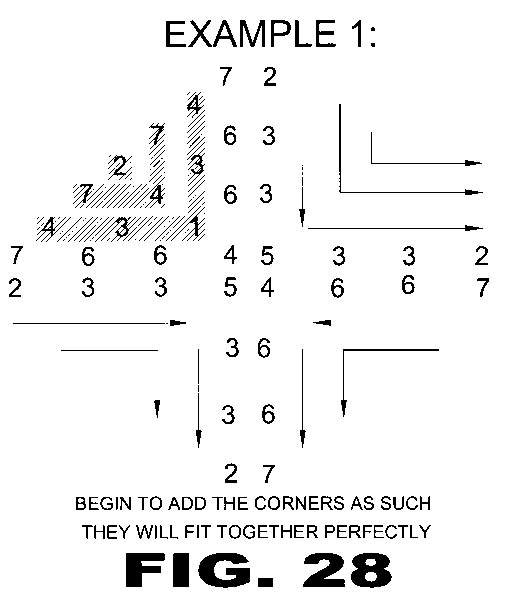
| FIGURE 28 Figure 28 are examples of the present invention. |
|
 |
|
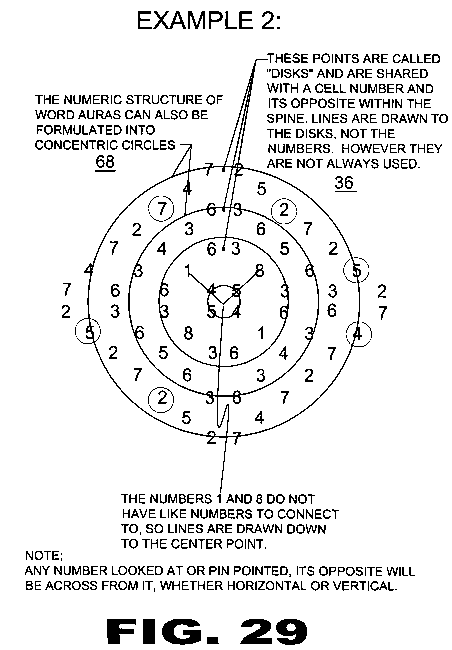
| FIGURE 29 Figure 29 are examples of the present invention. |
|
 |
|
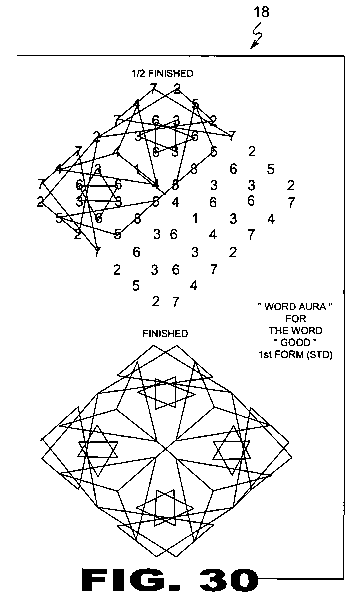
| FIGURE 30 Figure 30 are examples of the present invention. |
|
 |
|
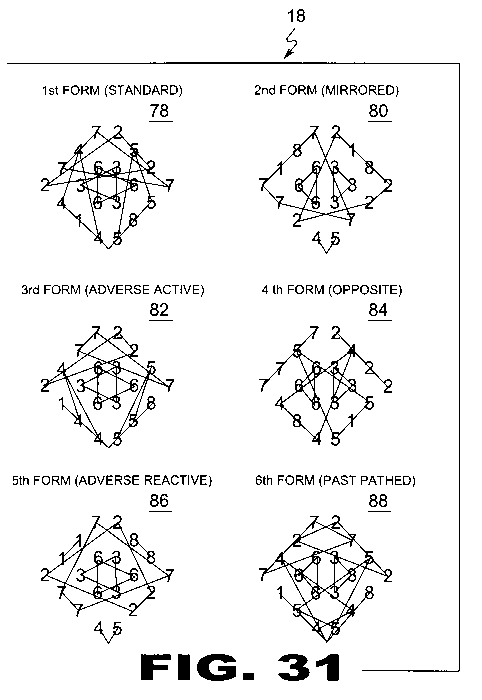
| FIGURE 31 Figure 31 are examples of the present invention. There are six individual adding formulas for making Word Auras (18). Each adding formula creates a different design. This can be illustrated by using only a quarter of the word aura. |
|
 |
|
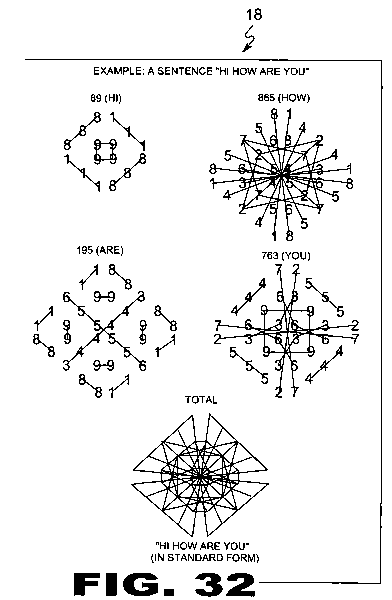
| FIGURE 32 Figure 32 are examples of the present invention. Word Auras (18) are a great way to send coded messages or information from one party to another. Separate Word Auras (18) can interlock to form one design. |
|
 |
|
| FIGURE 33 Figure 33 is an illustrative view of word aura code system of the present invention. Word Auras (18) are specifically designed to send short quick messages. They can be sent separately or fused together inside one another at the center point to conceal their individual structures. Word Auras (18) are a code system that can mutate much like a virus, and has the ability to shape shift depending on the adding formula it is in. However one can change the Cell Number (76) instead of the adding formula and come up with the same geometric shape. Using the word "god" as an example in the 1st form (std) and change the Cell Number (76) to the 3rd form (ada) which changes the word "god" into the word "joy". Note: different numbers, but maintains the same geometric design. |
| E-Mail patent@invention.net |